Vector DB

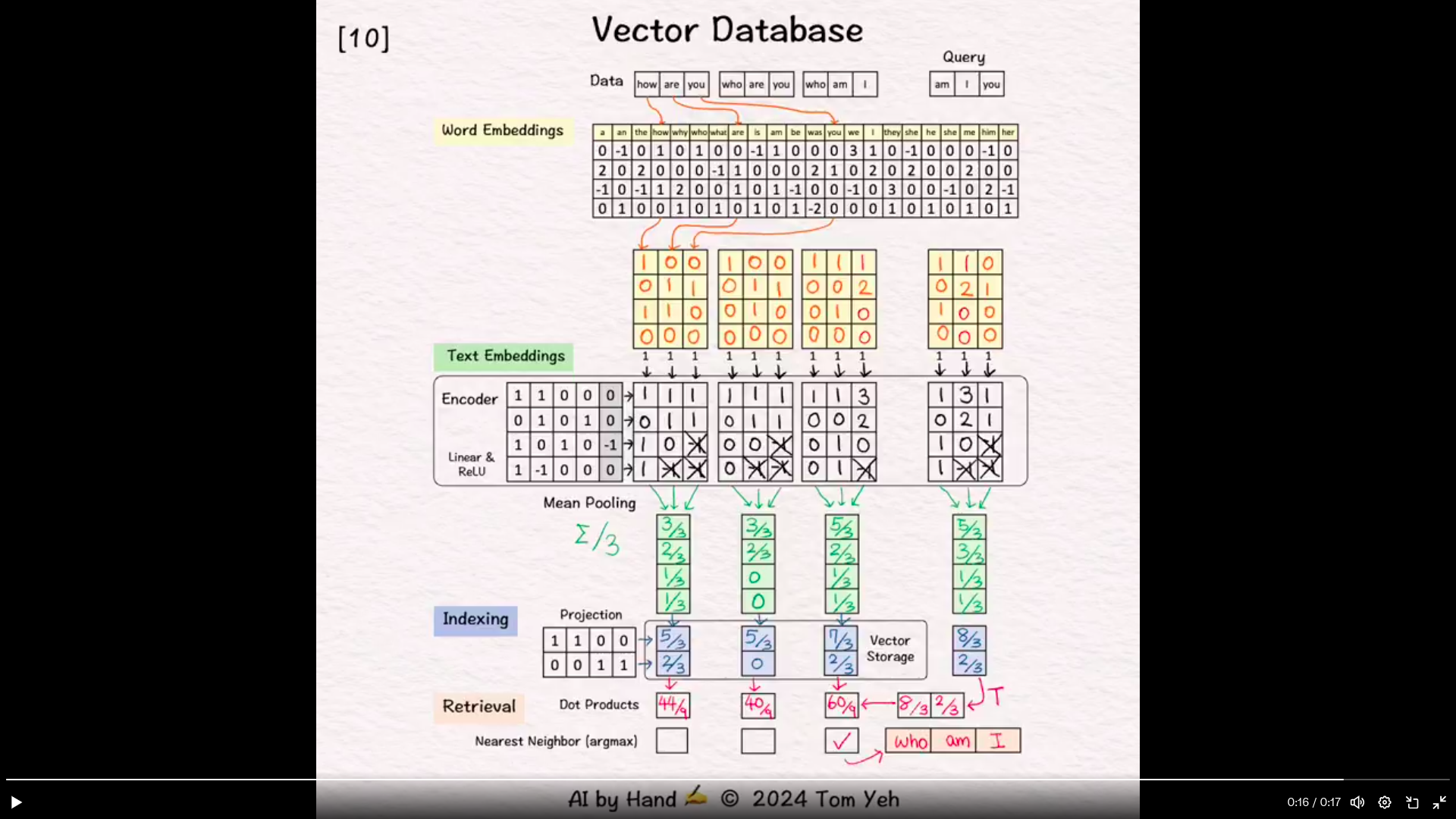
How it works

A dataset of three sentences, each has 3 words (or tokens)

• In practice, a dataset may contain millions or billions of sentences.
• The max number of tokens may be tens of thousands (e.g., 32,768 mistral-7b).

Process “how are you”

Word Embeddings

• For each word, look up corresponding word embedding vector from a table of 22 vectors, where 22 is the vocabulary size.
• In practice, the vocabulary size can be tens of thousands. The word embedding dimensions are in the thousands (e.g., 1024, 4096)

Encoding

• Feed the sequence of word embeddings to an encoder to obtain a sequence of feature vectors, one per word.
• Here, the encoder is a simple one layer perceptron (linear layer + ReLU)
• In practice, the encoder is a transformer or one of its many variants.

Mean Pooling

• Merge the sequence of feature vectors into a single vector using “mean pooling” which is to average across the columns.
• The result is a single vector. We often call it “text embeddings” or “sentence embeddings.”
• Other pooling techniques are possible, such as CLS. But mean pooling is the most common.

Indexing

• Reduce the dimensions of the text embedding vector by a projection matrix. The reduction rate is 50% (4→2).
• In practice, the values in this projection matrix is much more random. The purpose is similar to that of hashing, which is to obtain a short representation to allow faster comparison and retrieval.
• The resulting dimension-reduced index vector is saved in the vector storage.

Process “who are you”

• Repeat Word Embeddings to indexing

Query: “am I you”

• Repeat Word Embeddings to indexing
• The result is a 2-d query vector.

Dot Products

• Take dot product between the query vector and database vectors. They are all 2-d.
• The purpose is to use dot product to estimate similarity.
• By transposing the query vector, this step becomes a matrix multiplication.

Nearest Neighbor

• Find the largest dot product by linear scan.
• The sentence with the highest dot product is “who am I”
• In practice, because scanning billions of vectors is slow, we use an Approximate Nearest Neighbor (ANN) algorithm like the Hierarchical Navigable Small Worlds (HNSW).

algorithms commonly used for similarity search indexing

• Product quantization (PQ)
• Locality sensitive hashing
• Hierarchical navigable small world (HNSW

How to reduce the optimize the vector embedding

• Principal component analysis : reduce the vector dimension and store but not efficient
• Matryoshka Representation Learning :
• Binary Quantization : quantization in models where you reduce the precision of weights, quantization for embeddings refers to a post-processing step for the embeddings themselves. In particular, binary quantization refers to the conversion of the float32 values in an embedding to 1-bit values, resulting in a 32x reduction in memory and storage usage.
• For more check here

DIfferet distance calculation algorithm

Metric	When to Use	Why to Use
Cosine Similarity	- Text data (e.g., TF-IDF, word embeddings)	- Measures the angle between vectors, ignoring magnitude
	- Document similarity, sentence comparison	- Focuses on the direction of vectors, useful for comparing content (e.g., semantic meaning)
	- High-dimensional, sparse data (e.g., NLP, recommender systems)	- Magnitude-insensitive, so works well with documents of different lengths or sparse features
Dot Product	- When both magnitude and direction are important	- Measures both magnitude and direction of vectors, useful when frequency or importance matters
	- Frequency-based vector representations (e.g., Bag-of-Words, TF)	- Computationally simpler than cosine similarity; no need for normalization if magnitudes matter
	- Quick similarity calculation (e.g., in recommendation systems)	- Sensitive to vector magnitude, works well for scoring based on term frequencies or numerical values
Euclidean Distance	- When the absolute difference between vectors is important (e.g., spatial data, feature vectors)	- Measures the straight-line distance between vectors in a space, sensitive to scale differences
	- Clustering, regression tasks, or other geometric distance-based problems	- Sensitive to scale; accounts for magnitude differences, great for real-valued, continuous data
	- Works well for dense vectors where absolute differences matter	- Intuitive interpretation as “distance” in space

Postgress Vector DB

• Integrated Vector Storage: Store your vectors seamlessly alongside your other data in PostgreSQL, leveraging the database’s robustness, ACID compliance, and recovery features.

• Versatile Search: pgvector supports both exact and approximate nearest neighbor searches, catering to various accuracy and speed requirements.

• Distance Functions: Offers a range of distance metrics, including L2 distance, inner product, cosine distance, L1 distance, Hamming distance, and Jaccard distance. This flexibility allows you to select the most appropriate measure for your data and task.

• Diverse Vector Types: Handles various vector formats, including single-precision, half-precision, binary, and sparse vectors, accommodating different use cases.

• Multilingual Accessibility: pgvector can be used with any programming language that has a PostgreSQL client, enabling you to work with vectors in your preferred environment.

• Enabling the Extension: Use the SQL command CREATE EXTENSION vector; to enable pgvector in your desired database.

• Creating a Vector Column: Define a vector column in your table using the vector(n) data type, where ‘n’ represents the number of dimensions.

• Inserting Vectors: Insert vectors as array-like strings, e.g., ”.

• Querying Nearest Neighbors: Employ distance operators like <-> for L2 distance, <#> for inner product, and <= > for cosine distance to find nearest neighbors, ordering results and limiting output as needed.

Supported distance functions are:

←> - L2 distance <#> - (negative) inner product ⇐> - cosine distance <+> - L1 distance <~> - Hamming distance (binary vectors) < %> - Jaccard distance (binary vectors)

Indexing and Performance Optimization

Three types of vector search indices available in PostgreSQL:

1.IVF Flat: Good for medium workloads, low memory usage, but requires rebuilding on updates and has lower accuracy compared to other options.

2.HNSW: A versatile, graph-based index suitable for real-time search on medium to large workloads, offering a good balance of speed and accuracy, handling updates efficiently, and supporting quantization. Drawbacks include high memory usage and potential scalability limitations with very large datasets.

3.Streaming Disk ANN: Excelent for real-time search and filtered search scenarios, particularly with large-scale workloads (10 million+ vectors). It offers high accuracy, scales effectively, supports quantization by default, and has cost advantages as its costs scale with disk and RAM rather than solely RAM. The main drawback is longer build times compared to HNSW

pgvector also offers various options to fine-tune indexing and querying performance:

• Index Parameters: Customize parameters like m (connections per layer) and ef_construction (candidate list size) for HNSW, and lists (number of inverted lists) for IVFFlat, to balance recall and build time.
• Query Options: Control search parameters like hnsw.ef_search (dynamic candidate list size for HNSW) and ivfflat.probes (number of lists to probe for IVFFlat) to adjust the speed-recall trade-off during query execution.
• Filtering Techniques: Employ techniques like creating indexes on filter columns, using multicolumn indexes, utilizing approximate indexes for selective filters, and considering partial indexing or partitioning for specific filtering scenarios to optimize performance.
• Iterative Index Scans: Introduced in pgvector 0.8.0, iterative scans improve recall for queries with filtering by progressively scanning more of the index.

pgvector extends its capabilities beyond basic vector operations, supporting:

• Half-Precision Vectors: The halfvec type efficiently stores vectors using half-precision floating-point numbers, reducing storage requirements without significant loss of accuracy.
• Binary Vectors: pgvector can handle binary vectors using the bit data type, enabling efficient storage and querying for data represented in this format.
• Sparse Vectors: The sparsevec type effectively stores vectors with a large number of zero values, reducing storage and processing overhead.
• Hybrid Search: Combine pgvector’s vector similarity search with PostgreSQL’s full-text search to create powerful hybrid search systems for retrieving relevant data based on both semantic meaning and vector representations.
• Subvector Indexing: Index and query specific portions of vectors using expression indexing, facilitating specialized searches and analysis.

PgVectorScale and Pagai

pgvectorscale complements pgvector, the open-source vector data extension for PostgreSQL, and introduces the following key innovations for pgvector data:

• A new index type called StreamingDiskANN, inspired by the DiskANN algorithm, based on research from Microsoft.
• Statistical Binary Quantization: developed by Timescale researchers, This compression method improves on standard Binary Quantization.

pgai simplifies the process of building search, Retrieval Augmented Generation (RAG), and other AI applications with PostgreSQL. It complements popular extensions for vector search in PostgreSQL like pgvector and pgvectorscale, building on top of their capabilities.

Example

 
CREATE EXTENSION IF NOT EXISTS ai CASCADE ->will create the pgai extension
 
//will create embedding 
 
SELECT ai.create_vectorizer('{self.table_name}'::regclass,
destination => '{self.embedding_table_name}',
embedding => ai.embedding_openai('{st.session_state.embedding_model}', 768),
chunking => ai.chunking_recursive_character_text_splitter('content')
);
 

How pgai are work?

• Pgai are use the sql extension feature where they have written the function defintion in sql and which will interact with python script

Resources

• How We Made PostgreSQL as Fast as Pinecone for Vector Data
• PostgreSQL Hybrid Search Using Pgvector and Cohere
• Vector Similarity Search with PostgreSQL’s pgvector – A Deep Dive
• Build, scale, and manage user-facing Retrieval-Augmented Generation applications using postgress
• Learn to build vector-powered systems with VectorHub, a free education and open-source platform for data scientists.

All vector db in one place https://superlinked.com/vector-db-comparison

Qudrant

Concepts

• Collections: A collection is a named set of points (vectors with a payload) among which you can search. The vector of each point within the same collection must have the same dimensionality and be compared by a single metric. Named vectors can be used to have multiple vectors in a single point, each of which can have their own dimensionality and metric requirements.

• Distance Metrics: These are used to measure similarities among vectors and they must be selected at the same time you are creating a collection. The choice of metric depends on the way the vectors were obtained and, in particular, on the neural network that will be used to encode new queries.

• Points: The points are the central entity that Qdrant operates with and they consist of a vector and an optional id and payload. (smilar to documents in mogodb)

  • id: a unique identifier for your vectors.
  • Vector: a high-dimensional representation of data, for example, an image, a sound, a document, a video, etc.
  • Payload: A payload is a JSON object with additional data you can add to a vector.

• Storage : Qdrant can use one of two options for storage, In-memory storage (Stores all vectors in RAM, has the highest speed since disk access is required only for persistence), or Memmap storage, (creates a virtual address space associated with the file on disk).

Qdrant supports these most popular types of metrics:

• Dot product: Dot 
• Cosine similarity: Cosine 
• Euclidean distance: Euclid 
• Manhattan distance: Manhattan 

collections

Creating a collection involves specifying parameters like vector size, distance metric, and various configuration options

PUT /collections/{collection_name}
{
    "vectors": {
      "size": 100,
      "distance": "Cosine"
    },
    "init_from": {
       "collection": "{from_collection_name}"
    }
}

Point

A document in db

PUT /collections/{collection_name}/points
{
    "points": [
        {
            "id": 1,
            "payload": {"color": "red"},
            "vector": [0.9, 0.1, 0.1]
        }
    ]
}

Each point in qdrant may have one or more vectors.Supported vector types

• Dense Vectors → Generated by LLM

• Sparse Vectors → Vectors with no fixed length, but only a few non-zero elements. Useful for exact token match and collaborative filtering recommendations.

• MultiVectors → Matrices of numbers with fixed length but variable height. Usually obtained from late interraction models like ColBERT.

If the collection was created with multiple vectors, each vector data can be provided using the vector’s name:

PUT /collections/{collection_name}/points
{
    "points": [
        {
            "id": 1,
            "vector": {
                "image": [0.9, 0.1, 0.1, 0.2],
                "text": [0.4, 0.7, 0.1, 0.8, 0.1, 0.1, 0.9, 0.2]
            }
        },
        {
            "id": 2,
            "vector": {
                "image": [0.2, 0.1, 0.3, 0.9],
                "text": [0.5, 0.2, 0.7, 0.4, 0.7, 0.2, 0.3, 0.9]
            }
        }
    ]
}

https://milvus.io/
https://qdrant.tech/ https://weaviate.io/